In mathematics and computer science, an algorithm is a step-by-step procedure for calculations. Algorithms are used for calculation, data processing, and automated reasoning.
The Algorithms Group brings together academics at UNSW with research interests in algorithms and complexity.
Algorithms are at the heart of all information processing. We design and analyse algorithms in terms of resource requirements (time, space, randomness) and we study their limitations. Research in this field emphasizes mathematical technique and rigor.
Multivariate complexity. An important focus of our group is multivariate complexity analysis and algorithm design, a.k.a. parameterized complexity. The basic insight is that in many situations, one or more secondary measurements of problem instances or computational objectives, beyond the overall input size, govern a problem's computational complexity.
• FPT News • FPT Wiki •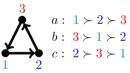
Computational Social Choice. This focus area studies algorithmic and computational aspects of combining individual preferences and interests into collective decisions. It encompassed coalition formation, preference aggregation, ranking systems, resource allocation, and voting.
• Computational Social Choice Website • PrefLib •
Optimisation. Our group focuses on several areas in optimisation, and in particular discrete optimisation. Our work includes algorithms for coloring, constraint satisfaction, global constraints, scheduling, and Satisfiability.
• Global Constraint Catalog • SAT Live! •