| COMP1011 Assignment 2 - 05s2 | |
|---|---|
| Computing 1A 05s2 |
Last updated
Thu 13 Oct 2005 15:53
Mail cs1011@cse.unsw.edu.au |
Scalar is simply a mathematical term for a value that is not a compound value. e.g. 3. Often mathematicians will talk of multiplying a vector by a scalar. This simply means that each component of the vector is multipled by the scalar.
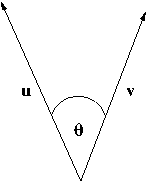
Vectors can be multiplied in two different ways. Refer the the following figure in the following two sections.

The dot product of a pair of vectors u = (ux, uy,uz) and v = (vx, vy,vz) is defined to be:
u·v = uxvx + uyvy + uzvz
This is not a vector, it is a scalar. It is also the case that:
u·v = |u||v|cos
&theta
where &theta is the angle between the vectors and
|w| is the magnitude of a vector w.
In the case of unit vectors which have a magnitude of one one can see clearly that u·v = cos &theta.
It is thus, quite easy to find the angle between two vectors using
the dot product and you will see that we have done so in module
Physics.
Unlike the dot product, the cross product of two vectors is another vector. This vector points in a direction that is perpendicular to the other two. Obviously there are two ways for this to occur. If we view the two vectors as being in the same plane the resulting vector could point out of either the front or the back face.
Which direction it does point depends on the relative directions of the two vectors. If the second vector is clockwise with respect to the first in the plane then the vector points towards us. Otherwise it points away from us. This is illustrated in the following figure (where u x v = w):
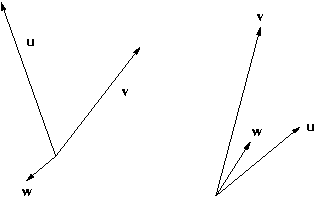
In the left diagram, v is clockwise with respect to u and so w points towards us. On the right, v is anti-clockwise with respect to u and so w points away from us.
Now for the definition of the cross product:
u x v = |u||v|sin &theta
n
where &theta is the angle between u and
v and n is a unit vector in the direction
perpendicular to both u and v subject
to the figure above.
It is also the case that:
u x v = (uyvz - uzvy, uzvx - uxvz, uxvy - uyvx)
Another way to think of n is as the vector that
defines the plane in which u and
v lie. This is particularly useful if you wish to
rotate a vector within a plane. We have provided a function called
rotateInPlane in module (you guessed it) Physics which takes a unit vector
defining a plane, a vector to be rotated, and an angle and rotates the
vector in that plane. See the module for more details.