OctTrees: Making ray tracing more efficient

Despite the simplicity of the algorithm, ray tracing is a computationally intensive process. Depending on the complexity of the scene it can take hours to create a single image. One of the things that slows down the algorithm, especially in scenes containing many objects is that, for each ray, intersection is tested against every single object. Clearly, this can lead to much redundant computation. Imagine a row of non-overlapping spheres parallel with the x-y plane. Each ray from the eye only intersects one of these spheres. Now imagine there are thousands of them.

The solution to this conundrum is to split up three dimensional space into smaller chunks, each of which is guaranteed to contain at most a small number of objects. One particularly elegant way of doing this is using OctTrees: a structure that recursively sub-divides voxels (which are cubes) in eight smaller voxels. But before we can talk about how to create an OctTree we must first talk about what it means for an object to be contained within a voxel.

An object is considered to be contained within a voxel if any portion of its surface is inside. For example a voxel could completely contain a sphere, or only part of its surface could intersect with the front face. Yet, if a voxel happens to be completely contain within a sphere then we do not say that the voxel contains the sphere. We have provided a function in the WorldBase module called contains which checks whether an object is contained within a voxel or not.

With that explained we can now explain the subdivision process. We start with one large voxel containing the scene and a maximum number of objects that we wish each voxel to contain. We shall call this maxObjects. If the voxel contains at most maxObjects objects then we are done; no further subdivision is required. This voxel becomes a leaf of the OctTree and contains all the objects. If, on the other hand, there are more we divide the voxel into eight smaller and equally sized voxels as per Figure 1. Each one of these is known as an octant of the original voxel. We create a node in the OctTree that will hold eight smaller OctTrees, which will be created from the octants.

We then repeat the process. For each of the eight voxels we check whether they have more than maxObjects contained within them. For those that do, we sub-divide and repeat the process again. For those that don't, we stop. The process terminates when no voxel contains more than maxObjects objects.

Thus, we can see that OctTrees break up three dimensional space is a non-uniform way. The greatest number of leaves of the OctTree will be clustered around the part of the scene where the most objects are.

Example

Figure 2 shows a pictorial example of an OctTree:

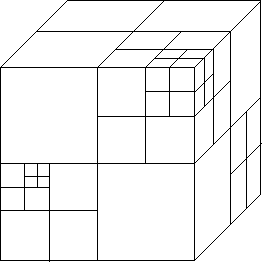
Figure 2. One possible OctTree

The advantage of using OctTrees is that now there are a lot less objects to check intersections against. The process of ray tracing also changes in a subtle way. When we fire a ray from the eye we must first find what leaf of the OctTree we are in. We then check for intersections in that voxel. However, if we don't find an intersection this does not mean that there are no more. There could be more in other leaves of the OctTree that the ray passes through. What is needed is some way in which to find the next leaf we should be checking.

We provide a function called pointNextVoxel in module WorldBase which returns a point that is guaranteed to be in the next leaf of the OctTree that contains the ray. It requires, as one of its arguments, the minimum size of all the leaves in the OctTree. You will have to write a function findMinSize to calculate this value.

pointNextVoxel is not enough to find the next leaf; one also needs a function getLeafContaining which finds the leaf containing the point. You will also be writing this function.

This process of checking for intersections and moving on to the next leaf of the OctTree is repeated until an intersection is found or the ray passes out of the bounding voxel of the scene. This is easily checked for.

A good question is, for a given voxel what are the points that are contained within it? The answer is obvious for points well inside the voxel, but what about points on the faces? Are they included? Sometimes and sometimes not. The voxel contains all those points that are on the bottom, left and front faces but not those on the top, right and back faces.

Check the code of isInVoxel in WorldBase for more details.