Week 08

Recursion 1/42

A recursive function is one that calls itself within the program text

int factorial(int n) {  // recursive version      
	int retval;
	if (n == 0) {
		retval = 1;
	} else {
		retval = n * factorial(n-1);
	}
	return retval;

Mathematical definitions often lend themselves directly to a recursive implementation.

0! = 1
n! = n * (n-1)! , for n>0

... Recursion 2/42

Exercise
Use a recursive function to implement Euclid's algorithm for computing the greatest common divisor

gcd(a,b) = a , if a=b
gcd(a,b) = gcd(a-b,b) , if a>b
gcd(a,b) = gcd(a,b-a) , if a<b


gcd(651,378) = gcd(273,378)
             = gcd(273,105)
             = gcd(168,105)
             = gcd(63,105)
             = gcd(63,42)
             = gcd(21,42)
             = gcd(21,21)
             = 21

... Recursion 3/42

Most list functions can be implemented recursively

length(L) = 0 , if L empty

length(L) = length(L->next) + 1 , otherwise

int length(List L) {      // recusive version
	int retval;
	if (L == NULL) {  // base case
		retval = 0;
	} else {          // recursive case
		retval = length(L->next) + 1;
	}
	return retval;
}

... Recursion 4/42

// Search for item in sorted int list
// Returns pointer to node, or NULL if not found
Node *search(SortedIntList L, int v) {
	Node *retval;
	if (L == NULL) {
		retval = NULL;
	} else if (v < L->value) { // v can't be in the list       
		retval = NULL;     
	} else if (v > L->value) { // recursive case
		retval = search(L->next, v);
	} else { // found
		retval = L;
	}
	return retval;
}

Exercise Write recursive functions to insert/delete a list element

Node *insert(SortedIntList, int);
Node *delete(SortedIntList, int);

Data Structures 5/42

Structured data objects

consist of a collection of elements
have operations to maintain/use the collection

An element can be

a simple value (e.g. integer or string)
a structured value
- perhaps a sub-collection (hierarchical data structures)
- a record with multiple values (e.g. C struct)
  possibly with an identifying key (e.g. student id)

... Data Structures 6/42

Typical operations on a data structure

create an empty collection
add a new element to the collection (insert, push, enqueue)
remove an element from the collection (remove, pop, dequeue)
search for an element by content (or by key)
traverse/iterate over all elements (or a subset)
examine properties of the collection (size, state, ...)

A specific collection of operations defines one type of data structure.

... Data Structures 7/42

Data structures we have seen so far:

arrays (indexed linear sequence of homogeneous values)
structs (heterogeneous values, accessed by field name)
dynamic linear structures (linked lists, stacks, queues)

Other major classes of data structure:

dynamic branched structures (trees)
dynamic cyclic structures (graphs)

... Data Structures 8/42

Implementing Complex Structures 9/42

So far, we have looked at linear structures:

typedef struct node {
	ValueType value;
	struct node *next;
	// might also have *prev
} Node;
typedef Node *List;

One implementation of complex structures generalises this:

typedef struct node {
	ValueType value;
	struct node *neighbours[];
} Node;
typedef Node *Collection;

Binary Search Trees

Binary Trees 11/42

Binary trees are a type of dynamic data structure

developed primarily to improve search efficiency

Problem with searching in linked-lists:

start at first node, scan sequentially
stop when find a match or at end of list

Cost of searching in an unsorted list of length n

best: 1, worst: n, average: n/2

Binary trees can improve this to worst case: log₂n

Cost for list with 1000 nodes ... linear: 1000, binary tree: 10

... Binary Trees 12/42

Trees are branched dynamic data structures

each node contains a data value
each node contains links to k other nodes (k=2 below)

... Binary Trees 13/42

Trees can be viewed as a set of nested structures:

each node has k sub-trees
any/all subtrees may be empty (all empty → leaf)

... Binary Trees 14/42

Node level = path length from root to node

Tree height = max path length from root to leaf

Height of tree with n nodes: mi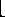n = log₂n 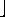, max = n-1

... Binary Trees 15/42

Trees are used in many contexts, e.g.

representing hierachical data structures (e.g. expressions)
efficient searching (e.g. sets, symbol tables, ...)

... Binary Trees 16/42

Search trees have the properties

all values in left subtree are less than root
all values in right subtree are greater than root
this property applies over all nodes in the tree

Balanced trees have the properties

#nodes in left subtree = #nodes in right subtree
this property applies over all nodes in the tree

... Binary Trees 17/42

Examples of binary search trees:

[Diagram:Pic/binary-search-trees-small.png]

Shape of tree is determined by order of insertion.

Exercise: Binary Search Trees 18/42

For each of the following sequences of values:

show the binary search tree that results
starting from an initially empty tree
and inserting them in the order given.

Sequences:

5, 3, 2, 7, 4, 6, 8
4, 2, 7, 9, 6, 8, 5, 1, 3
1, 2, 3, 4, 5, 6, 7, 8, 9

Representation of Binary Trees 19/42

Binary trees consist of Nodes, where each Node contains

a value
(we use int values in our examples, but could be any type)
pointer to left and right sub-trees
(more precisely, a pointer to the root node of each sub-tree)

typedef struct node {
	int value;
	struct node *left;
	struct node *right;
} Node; 
typedef Node *Tree;

A tree is represented by a pointer to its root node.

Operations on Binary Trees 20/42

For the rest of our discussion, we consider binary search trees.

A binary search tree type would typically have operations:

// make an empty tree
Tree emptyTree();

// insert a new value into the tree
Tree insert(Tree t, int v);

// delete a value from the tree
Tree delete(Tree t, int v);

// search for a value 
Node *search(Tree t, int v);

... Operations on Binary Trees 21/42

A useful auxiliary operation:

// Make a new Node
Node *newNode(int v) {
	Node *new;
	new = (Node *)malloc(sizeof(Node));
	assert(new != NULL);
	new->value = v;
	new->left = NULL;
	new->right = NULL;
	return new;
}

After creating such a Node it would typically be linked into a Tree.

Searching in Search Trees 22/42

Most tree algorithms are best described recursively

Example animation

// Search for item in tree
// Returns pointer to node, or NULL if not found
Node *search(Tree t, int  v) {
	Node *retval;
	if (t == NULL) {
		retval = NULL;
	} else if (v < t->value) {
		retval = search(t->left, v);
	} else if (v > t->value) {
		retval = search(t->right, v);
	} else { // found
		retval = t;
	}
	return retval;
}

Exercise: Count Nodes in a Binary Tree 23/42

Implement a function int size(Tree t)

that returns the number of nodes in a tree

Insertion into Search Trees 24/42

// Recursive version
// Insert into appropriate subtree
Tree insert(Tree t, int  v) {
	if (t == NULL)
		t = newNode(v);
	else if (v == t->value) {
		; // no duplicates allowed
	}
	else if (v < t->value) {
		t->left = insert(t->left, v);
	}
	else if (v > t->value) {
		t->right = insert(t->right, v);
	}
	return t;
}

... Insertion into Search Trees 25/42


// Non-recursive version
// Find location in tree; attach new leaf
void insert(Tree *t, int  v) {
	char lastTurn;
	Node *curr = *t;
	Node *parent = NULL;

	// empty tree; special case
	if (curr == NULL) {
		*t = newNode(v);
	} else {  // find where new leaf belongs
		while (curr != NULL) {
			if (v == curr->value) {
				; // no duplicates allowed
			} else if (v < curr->value) {
				parent = curr;
				curr = curr->left;
				lastTurn = 'L';
			} else if (v > curr->value) {
				parent = curr;
				curr = curr->right;
				lastTurn = 'R';
			}
		}
		// connect new node
		switch (lastTurn) {
		   case 'L': parent->left = newNode(v); break;
		   case 'R': parent->right = newNode(v); break;
		}
	}
}

Tree Traversal 26/42

For many traversals/iterations

we simply need to visit all elements in the collection
order of visiting elements is not important

For trees, several well-defined visiting orders exist:

preorder (NLR) ... visit root, then left subtree, then right subtree
inorder (LNR) ... visit left subtree, then root, then right subtree
postorder (LRN) ... visit left subtree, then right subtree, then root

... Tree Traversal 27/42

Consider visiting an expression tree like:

NLR: + * 1 3 - * 5 7 9    (useful for building tree)
LNR: 1 * 3 + 5 * 7 - 9    ("natural" order)
LRN: 1 3 * 5 7 * 9 - +    (useful for evaluation)

... Tree Traversal 28/42

Inorder traversal:

void TraverseLNR(Tree t) {
	if (t != NULL) {
		TraverseLNR(t->left);
		VISIT(t->value);
		TraverseLNR(t->right);
	}
}

where VISIT is some operation on the value in the Node

Exercise: Tree Traversal 29/42

Show NLR, LNR, LRN traversals for the following tree:

Tree Traversal 30/42

Traversal is a generic operation:

it would be useful to capture the generic notion
but be able specialise it to a specific operation

C provides a (limited) mechanism for this via function pointers.

Inorder traversal (with run-time choice of visit operation):

void TraverseLNR(Tree t, void (*visit)(int)) {
	if (t != NULL) {
		TraverseLNR(t->left, visit);
		(*visit)(t->value);
		TraverseLNR(t->right, visit);
	}
}

... Tree Traversal 31/42

Consider how we might use the above TraverseLNR()

void show(int v) {
	printf("%d ",v);
}

// ... which might be used as

Tree t;
...
TraverseLNR(t, show);

The second parameter has type pointer to function.

Deletion from BSTs

Deletion from Binary Search Trees 33/42

Insertion into a binary search tree is easy:

find location in tree where node to be added
create node and link to parent
always added as leaf, so only parent affected

Deletion from a binary search tree is harder:

find the node to be deleted and its parent
unlink node from parent; delete node
replace node in tree by ... ???

Example animation

... Deletion from Binary Search Trees 34/42

Case 1: value to be deleted is a leaf (zero subtrees)

... Deletion from Binary Search Trees 35/42

Case 1: value to be deleted is a leaf (zero subtrees)

... Deletion from Binary Search Trees 36/42

Case 2: value to be deleted has one subtree

... Deletion from Binary Search Trees 37/42

Case 2: value to be deleted has one subtree

... Deletion from Binary Search Trees 38/42

Case 3: value to be deleted has two subtrees

Replace deleted node by its immediate successor

... Deletion from Binary Search Trees 39/42

Case 3: value to be deleted has two subtrees

... Deletion from Binary Search Trees 40/42


Tree delete(Tree t, int v){
  if (t == NULL) {
    ; // v not found, nothing to do
  } else if (v < t->value) {   // delete v in left subtree
      t->left = delete(t->left, v);
  } else if (v > t->value) {   // delete v in right subtree
      t->right = delete(t->right, v);
  } else {
      // v == t->value, so the node 't' must be deleted
      // code below violates style, just to make logic clear
      Tree n;                                             // temporary
      if (t->left==NULL && t->right==NULL) n=NULL;        // 0 children
      else if (t->left ==NULL)             n=t->right;    // 1 child
      else if (t->right==NULL)             n=t->left;     // 1 child
      else                                 n=joinAtMinimum(t->left,t->right);
      free(t);
      t = n;
  }
  return t;
}

... Deletion from Binary Search Trees 41/42

// Joins t1 and t2 with the minimum of t2 as new root
Tree joinAtMinimum(Tree t1, Tree t2){
   Tree nuroot = t2;
   Tree p = NULL;
   while (nuroot->left != NULL) {
       p = nuroot;
       nuroot = nuroot->left;
   }                       // nuroot is the minimum, p is its parent
   if (p != NULL){
       p->left = nuroot->right; // give nuroot's only child to p
       nuroot->right = t2;      // nuroot replaces deleted node
   }
   nuroot->left = t1;           // nuroot replaces deleted node
   return nuroot;
}

Tips for Lab 42/42

Quacks, Recursion, Binary Search Trees

Use Quack ADT as stack for bracket matching
```
(a[i]+b[j])*c[k]
balanced

a(a+b]*c
unbalanced
```
- push open brackets
- when closing bracket found, pop and compare
Use recursion to reimplement a week 3 lab exercise (and 1 variation thereof)
Build, print, sum and free a BST
- Use newNode() and insert() from the lecture
- Write rescursive functions to print, sum and free the BST
Demonstrate that you've completed Stage 1 of the Assignment

Produced: 23 Sep 2015