Analysis of Algorithms ♢ COMP2521 ♢ (20T1)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [0/60]
An algorithm is a step-by-step procedure
- for solving a problem
- in a finite amount of time
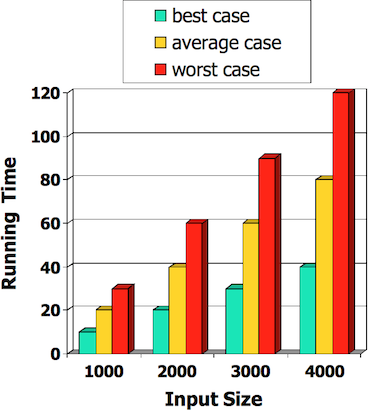
Most algorithms map input to output
- running time typically grows with input size
- average time often difficult to determine
- Focus on worst case running time
- easier to analyse
- crucial to many applications: finance, robotics, games, …
|
|
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [1/60]
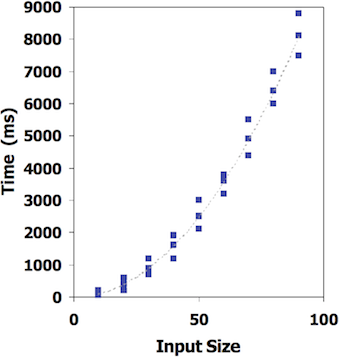
- Write program that implements an algorithm
- Run program with inputs of varying size and composition
- Measure the actual running time
- Plot the results
|
|
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [2/60]
Limitations:
- requires to implement the algorithm, which may be difficult
- results may not be indicative of running time on other inputs
- same hardware and operating system must be used in order to compare two algorithms
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [3/60]
- Uses high-level description of the algorithm instead of implementation ("pseudocode")
- Characterises running time as a function of the input size, n
- Takes into account all possible inputs
- Allows us to evaluate the speed of an algorithm independent of the hardware/software environment
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [4/60]
- More structured than English prose
- Less detailed than a program
- Preferred notation for describing algorithms
- Hides program design issues
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [5/60]
Example: Find maximal element in an array
arrayMax(A):
| Input array A of n integers
| Output maximum element of A
|
| currentMax=A[0]
| for all i=1..n-1 do
| | if A[i]>currentMax then
| | currentMax=A[i]
| | end if
| end for
| return currentMax
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [6/60]
Control flow
- if … then … [else] … end if
- while .. do … end while
repeat … until
for [all][each] .. do … end for
Function declaration
- f(arguments):
Input …
Output …
…
Expressions
- = assignment
- = equality testing
- n2 superscripts and other mathematical formatting allowed
- swap A[i] and A[j] verbal descriptions of simple operations allowed
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [7/60]
Formulate the following verbal description in pseudocode:
In the first phase, we iteratively pop all the elements from stack S and enqueue them in queue Q, then dequeue the element from Q and push them back onto S.
As a result, all the elements are now in reversed order on S.
In the second phase, we again pop all the elements from S, but this time we also look for the element x.
By again passing the elements through Q and back onto S, we reverse the reversal, thereby restoring the original order of the elements on S.
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [8/60]
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [9/60]
Implement the following pseudocode instructions in C
- A is an array of ints
...
swap A[i] and A[j]
...
-
head points to beginning of linked list
...
swap head and head->next
...
-
S is a stack
...
swap the top two elements on S
...
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [10/60]
-
int temp = A[i];
A[i] = A[j];
A[j] = temp;
-
NodeT *succ = head->next;
head->next = succ->next;
succ->next = head;
head = succ;
-
x = StackPop(S);
y = StackPop(S);
StackPush(S, x);
StackPush(S, y);
The following pseudocode instruction is problematic. Why?
...
swap the two elements at the front of queue Q
...
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [11/60]
RAM = Random Access Machine
- A CPU (central processing unit)
- A potentially unbounded bank of memory cells
- each of which can hold an arbitrary number, or character
- Memory cells are numbered, and accessing any one of them takes CPU time
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [12/60]
- Basic computations performed by an algorithm
- Identifiable in pseudocode
- Largely independent of the programming language
- Exact definition not important (we will shortly see why)
- Assumed to take a constant amount of time in the RAM model
Examples:
- evaluating an expression
- indexing into an array
- calling/returning from a function
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [13/60]
❖ Counting Primitive Operations | |
By inspecting the pseudocode …
- we can determine the maximum number of primitive operations executed by an algorithm
- as a function of the input size
Example:
arrayMax(A):
| Input array A of n integers
| Output maximum element of A
|
| currentMax=A[0] 1
| for all i=1..n-1 do n+(n-1)
| | if A[i]>currentMax then 2(n-1)
| | currentMax=A[i] n-1
| | end if
| end for
| return currentMax 1
-------
Total 5n-2
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [14/60]
❖ Estimating Running Times | |
Algorithm arrayMax requires 5n – 2 primitive operations in the worst case
- best case requires 4n – 1 operations (why?)
Define:
- a … time taken by the fastest primitive operation
- b … time taken by the slowest primitive operation
Let
T(n) be worst-case time of
arrayMax. Then
a·(5n - 2) ≤ T(n) ≤ b·(5n - 2)
Hence, the running time T(n) is bound by two linear functions
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [15/60]
❖ ... Estimating Running Times | |
Seven commonly encountered functions for algorithm analysis
- Constant ≅ 1
- Logarithmic ≅ log n
- Linear ≅ n
- N-Log-N ≅ n log n
- Quadratic ≅ n2
- Cubic ≅ n3
- Exponential ≅ 2n
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [16/60]
❖ ... Estimating Running Times | |
In a log-log chart, the slope of the line corresponds to the growth rate of the function
See the following chart :
http://bigocheatsheet.com/
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [17/60]
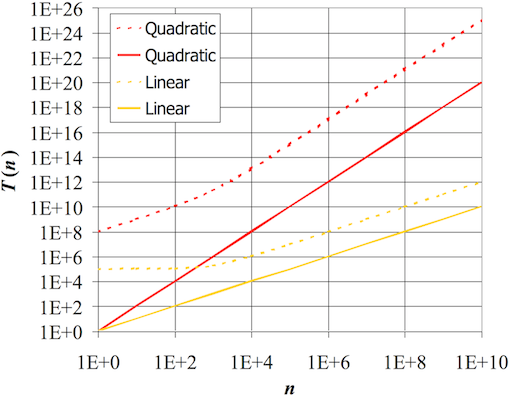
❖ ... Estimating Running Times | |
The growth rate is not affected by constant factors or lower-order terms
- Examples:
- 102n + 105 is a linear function
- 105n2 + 108n is a quadratic function
|
|
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [18/60]
❖ ... Estimating Running Times | |
Changing the hardware/software environment
- affects T(n) by a constant factor
- but does not alter the growth rate of T(n)
⇒ Linear growth rate of the running time T(n) is an intrinsic property of algorithm arrayMax
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [19/60]
❖ Exercise : Estimating running times | |
Determine the number of primitive operations
matrixProduct(A,B):
| Input n×n matrices A, B
| Output n×n matrix A·B
|
| for all i=1..n do
| | for all j=1..n do
| | | C[i,j]=0
| | | for all k=1..n do
| | | C[i,j]=C[i,j]+A[i,k]·B[k,j]
| | | end for
| | end for
| end for
| return C
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [20/60]
❖ Exercise : Estimating running times | |
matrixProduct(A,B):
| Input n×n matrices A, B
| Output n×n matrix A·B
|
| for all i=1..n do 2n+1
| | for all j=1..n do n(2n+1)
| | | C[i,j]=0 n2
| | | for all k=1..n do n2(2n+1)
| | | C[i,j]=C[i,j]+A[i,k]·B[k,j] n3·5
| | | end for
| | end for
| end for
| return C 1
------------
Total 7n3+4n2+3n+2
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [21/60]
Given functions f(n) and g(n), we say that
f(n) is O(g(n))
if there are positive constants c and n0 such that
f(n) ≤ c·g(n) ∀n ≥ n0
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [22/60]
Example: function 2n + 10 is O(n)
- 2n+10 ≤ c·n
⇒ (c-2)n ≥ 10
⇒ n ≥ 10/(c-2)
- pick c=3 and n0=10
|
|
|
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [23/60]
Example: function n2 is not O(n)
- n2 ≤ c·n
⇒ n ≤ c
- inequality cannot be satisfied since c must be a constant
|
|
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [24/60]
Show that
- 7n-2 is O(n)
- 3n3 + 20n2 + 5 is O(n3)
- 3·log n + 5 is O(log n)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [25/60]
- 7n-2 is O(n)
need c>0 and n0≥1 such that 7n-2 ≤ c·n for n≥n0
⇒ true for c=7 and n0=1
- 3n3 + 20n2 + 5 is O(n3)
need c>0 and n0≥1 such that 3n3+20n2+5 ≤ c·n3 for n≥n0
⇒ true for c=4 and n0=21
- 3·log n + 5 is O(log n)
need c>0 and n0≥1 such that 3·log n+5 ≤ c·log n for n≥n0
⇒ true for c=8 and n0=2
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [26/60]
❖ Big-Oh and Rate of Growth | |
- Big-Oh notation gives an upper bound on the growth rate of a function
- "f(n) is O(g(n))" means growth rate of f(n) no more than growth rate of g(n)
- use big-Oh to rank functions according to their rate of growth
| f(n) is O(g(n)) | g(n) is O(f(n)) |
| g(n) grows faster | yes | no |
| f(n) grows faster | no | yes |
| same order of growth | yes | yes |
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [27/60]
- If f(n) is a polynomial of degree d ⇒ f(n) is O(nd)
- lower-order terms are ignored
- constant factors are ignored
- Use the smallest possible class of functions
- say "2n is O(n)" instead of "2n is O(n2)"
- Use the simplest expression of the class
- say "3n + 5 is O(n)" instead of "3n + 5 is O(3n)"
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [28/60]
Show that `sum_(i=1)^n i` is O(n2)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [29/60]
`sum_(i=1)^ni = (n(n+1))/2 = (n^2+n)/2`
which is O(n2)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [30/60]
❖ Asymptotic Analysis of Algorithms | |
Asymptotic analysis of algorithms determines running time in big-Oh notation:
- find worst-case number of primitive operations as a function of input size
- express this function using big-Oh notation
Example:
- algorithm
arrayMax executes at most 5n – 2 primitive operations
⇒ algorithm arrayMax "runs in O(n) time"
Constant factors and lower-order terms eventually dropped
⇒ can disregard them when counting primitive operations
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [31/60]
❖ Example: Computing Prefix Averages | |
NB. computing the array A of prefix averages of another array X has applications in financial analysis
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [32/60]
❖ ... Example: Computing Prefix Averages | |
A quadratic alogrithm to compute prefix averages:
prefixAverages1(X):
| Input array X of n integers
| Output array A of prefix averages of X
|
| for all i=0..n-1 do O(n)
| | s=X[0] O(n)
| | for all j=1..i do O(n2)
| | s=s+X[j] O(n2)
| | end for
| | A[i]=s/(i+1) O(n)
| end for
| return A O(1)
2·O(n2) + 3·O(n) + O(1) = O(n2)
⇒ Time complexity of algorithm prefixAverages1 is O(n2)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [33/60]
❖ ... Example: Computing Prefix Averages | |
The following algorithm computes prefix averages by keeping a running sum:
prefixAverages2(X):
| Input array X of n integers
| Output array A of prefix averages of X
|
| s=0
| for all i=0..n-1 do O(n)
| s=s+X[i] O(n)
| A[i]=s/(i+1) O(n)
| end for
| return A O(1)
Thus, prefixAverages2 is O(n)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [34/60]
The following recursive algorithm searches for a value in a sorted array:
search(v,a,lo,hi):
| Input value v
| array a[lo..hi] of values
| Output true if v in a[lo..hi]
| false otherwise
|
| mid=(lo+hi)/2
| if lo>hi then return false
| if a[mid]=v then
| return true
| else if a[mid]<v then
| return search(v,a,mid+1,hi)
| else
| return search(v,a,lo,mid-1)
| end if
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [35/60]
❖ ... Example: Binary Search | |
Successful search for a value of 8:
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [36/60]
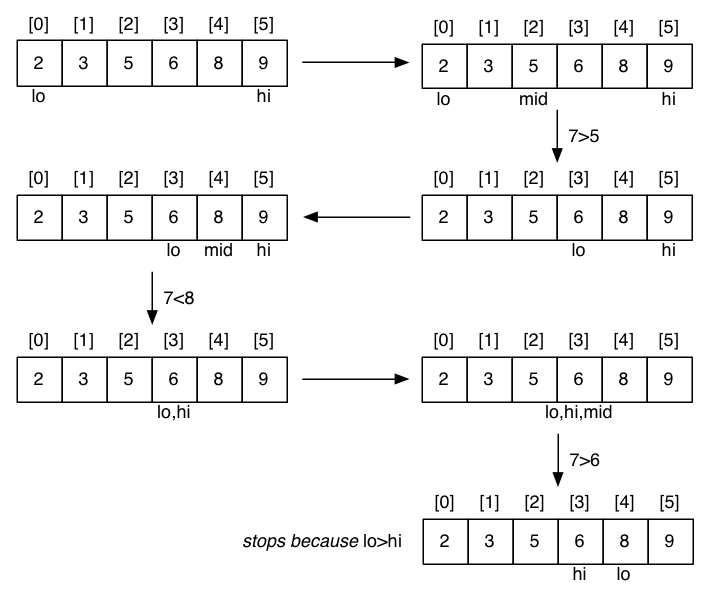
❖ ... Example: Binary Search | |
Unsuccessful search for a value of 7:
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [37/60]
❖ ... Example: Binary Search | |
Cost analysis:
- Ci = #calls to
search() for array of length i
- for best case, Cn = 1
- for
a[i..j], j<i (length=0)
- for
a[i..j], i≤j (length=n)
- Cn = 1 + Cn/2 ⇒ Cn = log2 n
Thus, binary search is O(log
2 n) or simply O(log n)
(why?)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [38/60]
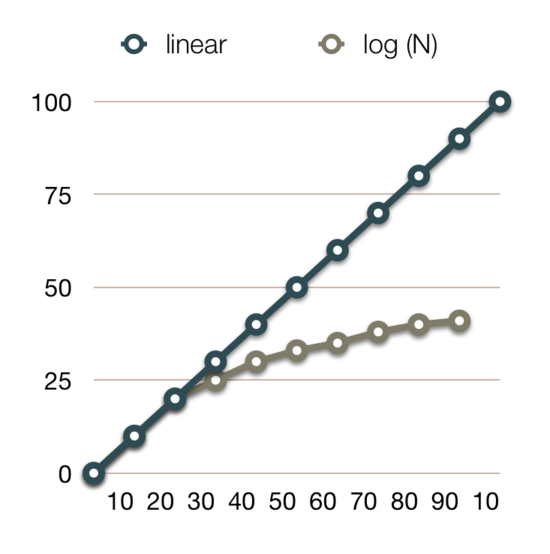
❖ ... Example: Binary Search | |
Why logarithmic complexity is good:
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [39/60]
❖ Math Needed for Complexity Analysi | |
- Summations
- Logarithms
- logb (xy) = logb x + logb y
- logb (x/y) = logb x - logb y
- logb xa = a logb x
- logb a = logx a / logx b
|
- Exponentials
- a(b+c) = abac
- abc = (ab)c
- ab / ac = a(b-c)
- b = alogab
- bc = ac·logab
|
- Proof techniques
- Summation (addition of sequences of numbers)
- Basic probability (for average case analysis, randomised algorithms)
|
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [40/60]
❖ Exercise : Analysis of Algorithms | |
What is the complexity of the following algorithm?
splitList(L):
| Input non-empty linked list L
| Output L split into two halves
|
|
| slow=head(L), fast=head(L).next
| while fast≠NULL ∧ fast.next≠NULL do
| slow=slow.next, fast=fast.next.next
| end while
| cut L between slow and slow.next
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [41/60]
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [42/60]
❖ Exercise : Analysis of Algorithms | |
What is the complexity of the following algorithm?
binaryConversion(n):
| Input positive integer n
| Output binary representation of n on a stack
|
| create empty stack S
| while n>0 do
| | push (n mod 2) onto S
| | n= n/2
n/2 | end while
| return S
| end while
| return S
Assume that creating a stack and pushing an element both are O(1) operations
("constant")
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [43/60]
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [44/60]
big-Omega
- f(n) is Ω(g(n)) if there is a constant c > 0 and an integer constant n0 ≥ 1 such that
f(n) ≥ c·g(n) ∀n ≥ n0
big-Theta
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [45/60]
❖ ... Relatives of Big-Oh | |
- f(n) is O(g(n)) if f(n) is asymptotically less than or equal to g(n)
- f(n) is Ω(g(n)) if f(n) is asymptotically greater than or equal to g(n)
- f(n) is Θ(g(n)) if f(n) is asymptotically equal to g(n)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [46/60]
❖ ... Relatives of Big-Oh | |
Examples:
- ¼n2 is Ω(n2)
- need c > 0 and n0 ≥ 1 such that ¼n2 ≥ c·n2 for n≥n0
- let c=¼ and n0=1
- ¼n2 is Ω(n)
- need c > 0 and n0 ≥ 1 such that ¼n2 ≥ c·n for n≥n0
- let c=1 and n0=2
- ¼n2 is Θ(n2)
- since ¼n2 is in Ω(n2) and O(n2)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [47/60]
Problems in Computer Science …
- some have polynomial worst-case performance (e.g. n2)
- some have exponential worst-case performance (e.g. 2n)
Classes of problems:
- P = problems for which an algorithm can compute answer in polynomial time
- NP = includes problems for which no P algorithm is known
Beware: NP stands for "nondeterministic, polynomial time (on a theoretical Turing Machine)"
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [48/60]
Computer Science jargon for difficulty:
- tractable … have a polynomial-time algorithm (useful in practice)
- intractable … no tractable algorithm is known (feasible only for small n)
- non-computable … no algorithm can exist
Computational complexity theory deals with different degrees of intractability
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [49/60]
❖ Generate and Test Algorithms | |
In scenarios where
- it is simple to test whether a given state is a solution
- it is easy to generate new states
(preferably likely solutions)
then a
generate and test strategy can be used.
It is necessary that states are generated systematically
- so that we are guaranteed to find a solution, or know that none exists
-
some randomised algorithms do not require this, however
(more on this later in this course)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [50/60]
❖ ... Generate and Test Algorithms | |
Simple example: checking whether an integer n is prime
- generate/test all possible factors of n
- if none of them pass the test ⇒ n is prime
Generation is straightforward:
- produce a sequence of all numbers from 2 to n-1
Testing is also straightfoward:
- check whether next number divides n exactly
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [51/60]
❖ ... Generate and Test Algorithms | |
Function for primality checking:
isPrime(n):
| Input natural number n
| Output true if n prime, false otherwise
|
| for all i=2..n-1 do
| | if n mod i = 0 then
| | return false
| | end if
| end for
| return true
Complexity of isPrime is O(n)
Can be optimised: check only numbers between 2 and `|__sqrt n__|` ⇒ O(`sqrt n`)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [52/60]
Problem to solve ...
Is there a subset S of these numbers with sum(S)=1000?
34, 38, 39, 43, 55, 66, 67, 84, 85, 91,
101, 117, 128, 138, 165, 168, 169, 182, 184, 186,
234, 238, 241, 276, 279, 288, 386, 387, 388, 389
General problem:
- given n integers and a target sum k
- is there a subset that adds up to exactly k?
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [53/60]
❖ ... Example: Subset Sum | |
Generate and test approach:
subsetsum(A,k):
| Input set A of n integers, target sum k
| Output true if Σb∈Bb=k for some B⊆A
| false otherwise
|
| for each subset S⊆A do
| | if sum(S)=k then
| | return true
| | end if
| end for
| return false
- How many subsets are there of n elements?
- How could we generate them?
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [54/60]
❖ ... Example: Subset Sum | |
Given: a set of n distinct integers in an array A …
- produce all subsets of these integers
A method to generate subsets:
- represent sets as n bits
(e.g. n=4,
0000, 0011, 1111 etc.)
- bit i represents the i th input number
- if bit i is set to 1, then
A[i] is in the subset
- if bit i is set to 0, then
A[i] is not in the subset
- e.g. if
A[]=={1,2,3,5} then 0011 represents {1,2}
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [55/60]
❖ ... Example: Subset Sum | |
Algorithm:
subsetsum1(A,k):
| Input set A of n integers, target sum k
| Output true if Σb∈Bb=k for some B⊆A
| false otherwise
|
| for s=0..2n-1 do
| | if k = Σ(ith bit of s is 1) A[i] then
| | return true
| | end if
| end for
| return false
Obviously,
subsetsum1 is O(2
n)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [56/60]
❖ ... Example: Subset Sum | |
Alternative approach …
subsetsum2(A,n,k)
(returns true if any subset of A[0..n-1] sums to k; returns false otherwise)
- if the nth value A[n-1] is part of a solution …
- then the first n-1 values must sum to k – A[n-1]
- if the nth value is not part of a solution …
- then the first n-1 values must sum to k
- base cases: k=0 (solved by {}); n=0 (unsolvable if k>0)
subsetsum2(A,n,k):
| Input array A, index n, target sum k
| Output true if some subset of A[0..n-1] sums up to k
| false otherwise
|
| if k=0 then
| return true
| else if n=0 then
| return false
| else
| return subsetsum(A,n-1,k-A[n-1]) ∨ subsetsum(A,n-1,k)
| end if
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [57/60]
❖ ... Example: Subset Sum | |
Cost analysis:
- Ci = #calls to
subsetsum2() for array of length i
- for best case, Cn = Cn-1 (why?)
- for worst case, Cn = 2·Cn-1 ⇒ Cn = 2n
Thus,
subsetsum2 also is O(2
n)
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [58/60]
❖ ... Example: Subset Sum | |
Subset Sum is typical member of the class of NP-complete problems
- intractable … only algorithms with exponential performance are known
- increase input size by 1, double the execution time
- increase input size by 100, it takes 2100 = 1,267,650,600,228,229,401,496,703,205,376 times as long to execute
- but if you can find a polynomial algorithm for Subset Sum,
then any other NP-complete problem becomes P !
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [59/60]
- Big-Oh notation
- Asymptotic analysis of algorithms
- Examples of algorithms with logarithmic, linear, polynomial, exponential complexity
- Suggested reading:
- Sedgewick, Ch.2.1-2.4,2.6
Analysis of Algorithms ♢ COMP2521 (20T1) ♢ Week 01b ♢ [60/60]
Produced: 5 Feb 2020
empty(S) do pop e from S, enqueue e into Q end while while
empty(Q) do dequeue e from Q, push e onto S end while found=false while
empty(S) do pop e from S, enqueue e into Q if e=x then found=true end if end while while
empty(Q) do dequeue e from Q, push e onto S end while
![[Diagram:Pic/growthFunctions.jpg]](Pic/growthFunctions.jpg)

![[Diagram:Pic/bigOh.png]](Pic/bigOh.png)
![[Diagram:Pic/bigOh-2.png]](Pic/bigOh-2.png)
n/2
| end while | return S