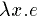|
Session 1, 2004
Exercises: Lambda Calculus
The following exercises should help you develop a better understanding
of how the lambda calculus works.
A note on notation: In the following, I use the Haskell syntax
\x -> e to denote lambda expressions  .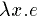
Translation of let-Bindings into the Plain Lambda
Calculus
In the lecture, we discussed that we can translate non-recusive and
recursive let bindings into the plain lambda calculus as follows:
| Non-recursive binding: |
|
let x = e1 in e2
|
|
|
=> |
(\x -> e2) e1
|
|
| Recursive binding: |
|
let x = e1 in e2
|
|
|
=> |
let x = fix (\x -> e1) in e2
|
where the fixed point
combinator fix is defined to be the function
fix :: (a -> a) -> a
fix f = f (fix f)
Your task is to find a translation rule for mutually recursive bindings
of the form
let {x1 = e1; ...;
xn = en}
in e
where the xi may occur in the
ei as well as in e. (Hint: It is
sufficient if you turn the set of mutually-recursive bindings into a
single recursive binding to which the previous rules can, then, be
applied.)
Translation of Data Constructors and case into the Plain
Lambda Calculus
In the lecture, we discussed that
pair = \a1 -> \a2 -> \sel -> sel a1 a2
fst = \p -> p (\a1 -> \a2 -> a1)
snd = \p -> p (\a1 -> \a2 -> a2)
encodes pair construction (pair) and decomposition
(fst and snd). In particular, the following
rules are satisfied:
fst (pair e1 e2) = e1
snd (pair e1 e2) = e2
Your tasks is to find an implementation of the constructors
nil and cons, the destructors
head and tail, and the conditional
ifNull, which encode lists and have to satisfy the
following rules:
head (cons e1 e2) = e1
tail (cons e1 e2) = e2
ifNull nil e3 e4 = e3
ifNull (cons e1 e2) e3 e4 = e4
Afterwards, implement the function
map f [] = []
map f (x:xs) = x : map f xs
in terms of nil, cons, head,
tail, and ifNull (without using
case, [], (:), or
pattern-matching).
|
