Homework 1, Thursday 1-3-2012

1. Consider a vending machine that accept pieces of 20 cents, 50 cents and 1 dollar, and that can dispense chocolate and pretzels, each of which costs 1 dollar. Draw an LTS whose transaction are labelled with "20c", "50c" or "$1", indicating the reception by the machine of a coin inserted by a user, and by the actions "chocolate" or "pretzel", indicating the opening of the glass door of the machine behind which chocolate or pretzels are stored. (We abstract from the closing of the door after extraction of the pretzel, which happens automatically, and the appearance of a new pretzel behind the glass door afterwards.) You may assume that the machine does not give change, and that it accepts any amount surplus money; alternatively you may assume that the opening for inserting coins will close after $1 or more has been inserted.

Homework 2, Thursday 8-3-2010

1. Draw a process graph for the ACP expression a(bc+b(c+d)).
2. Give an example of a process that has no completed traces at all.
3. A binary relation ~ on a set D is an equivalence relation if it is
   • reflexive: p ~ p for all processes p in D,
   • symmetric: if p ~ q then q ~ p,
   • and transitive: if p ~ q and q ~ r then p ~ r.
   1. Give an example of an equivalence relation on the domain of all people.
   2. Give 2 examples of a relation on people that is not an equivalence relation because exactly one of the three requirements above fails. Which one?
   3. If ~ is an equivalence relation on D, and p is in D, then [p]_~ denotes the set of all processes in D that are equivalent to p. Such a set is called an equivalence class. Show (formally, by means of a mathematical proof) that the collection of all equivalence classes form a partitioning of D. This means that every p in D belongs to one and only one equivalence class.
   [None of this has been treated in class; (c) is a test of prior mathematical exposure to the notion of a mathematical proof. If this is hard, it is a good warm-up for bits of mathematical proof yet to come.]
4. Let P be the process given by the recursive equation X = a.(b.X + c.X)
   and Q be the process (c+e).a. Assume an ACP communication function γ given by γ(a,c)=γ(c,a)=d.
   1. Draw a process graph representation of P and Q.
   2. Draw a process graph representation of P||Q.
   3. Draw a process graph representation of ∂_{a,c}(P||Q).
5. Give a formal definition of the sequential composition operator of ACP (see notes), in the style of the notes.

Homework 3, Thursday 15-3-2010

1. Give an example of two processes that have the same finite completed traces and the same finite partial traces, but not the same infinite traces.
2. Give an example of two processes without infinite traces that have the same partial traces but different completed traces.
3. For which possible choices of Q and R are there transitions of the form a.(c+b) | ((c+a) | b) --τ--> Q --τ--> R in the labelled transition system of CCS? Give a proof tree of the formal derivation of one of those transitions from the structural operational rules of CCS (found in today's handout).
   (CCS uses the communication function given by γ(a,a)=γ(a,a)=τ for all actions a.)
4. Sequencing is a binary operation defined on any process graphs; it starts with its second component as soon as its first component cannot do any further actions.
   Sequential composition, on the other hand, is defined on process graphs equipped with a state-labelling, where some states are marked with the symbol for successful termination, ✔. Here the second component starts only when the first one successfully terminates.
   1. Give a definition of sequencing as an operator on process graphs.
   2. Give an example that shows the difference between these two operators.
5. A partial equivalence is a relation that is symmetric and transitive.
   1. Give an example of a partial equivalence relation that is not an equivalence relation.
   2. If ~ is a partial equivalence relation on D, and s is in D, then [p]_~ denotes the set of all processes t in D satisfying s ~ t. Such a set is called a partial equivalence class. Show (formally, by means of a mathematical proof) that every element s of D belongs to at most one partial equivalence class.
   3. Do the equivalence classes always form a partition of D? Explain your answer.

Homework: Thursday 22-3-2012

1. Assume the following processes:

   X(data,dip)  =_def  send(mg(data,x)).Y()
   Y( ) =_def receive(m).( [m=mg(data,x) ∧ x=5] deliver(data).Y() +[m=mg(data,x) ∧ x≠5] X(data,x+1))

   • Describe the behaviour of X and Y in your own words.
   • Give labelled transition systems starting with the initial states Y() ⟨⟨ X(d,5) and Y() ⟨⟨ X(d,3), resp.
2. Give a sequential process defining a buffer for integers: the process should be ready to receive messages transferring an integer each. After a message has been received the integer should be stored in a queue. Last, the process should return to a state where it can receive the next message.
3. Extend the process derived in Part (2) by a non-deterministic choice. The process should not only be able to receive messages, it should also be able to synchronise with another sequential process running on the same node. If synchronisation occurs, the head of the queue should be transferred; moreover the first element of the queue should be dropped.
4. The next task is to define a process with a local variable count which receives a message containing an integer. Whenever an integer is received, it should be added to count.
5. Combine the processes derived in Part (3) and (4) in a way that they can exchange data. Give also a part of a labelled transition systems which shows synchronisation (you can choose the initial state).

head([1,5,7,2,3]) = 1
tail([1,5,7,2,3]) = [5,7,2,3]
append(17,[1,5,7,2,3]) = [1,5,7,2,3,17]

Please do not hesitate to contact me if you have any question or if you have trouble solving the homework.

Homework is due to April, 3rd. Please send your solution to peter.hoefner@nicta.com.au till noon, or bring it to the lecture.

Homework: Thursday 12-4-2012

1. Consider the following Büchi automaton:

   A1:

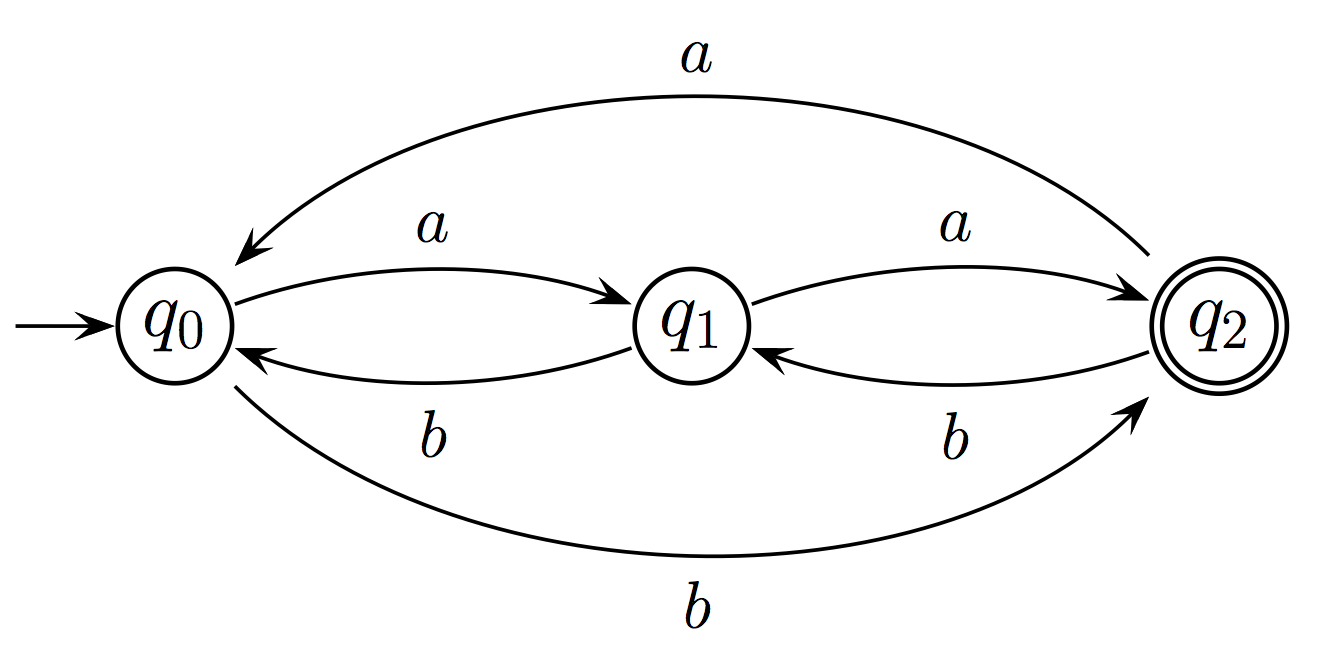   • Is it true that L(A₁)=∅?
   • Does A₁ accept a(b)^ω?
   • Does the automaton A₁ accept (abb)^ω? If it does, give an accepting run.
2. Assume Σ={a,b}. Define Büchi automata for the following languages:
   • L = {w | a occurs in w exactly once};
   • L = {w | after each a in w there is a b};
   • L = {w | a occurs on all even positions in w}.
3. Prove or disprove that the concatenation of a regular language and an ω-regular language is ω-regular. Here, concatenation is defined as usual as U.V = {u.v | u ∈ U , v ∈ V}, where u.v denotes word concatenation.
4. Consider the following two Büchi automata:

   A2:

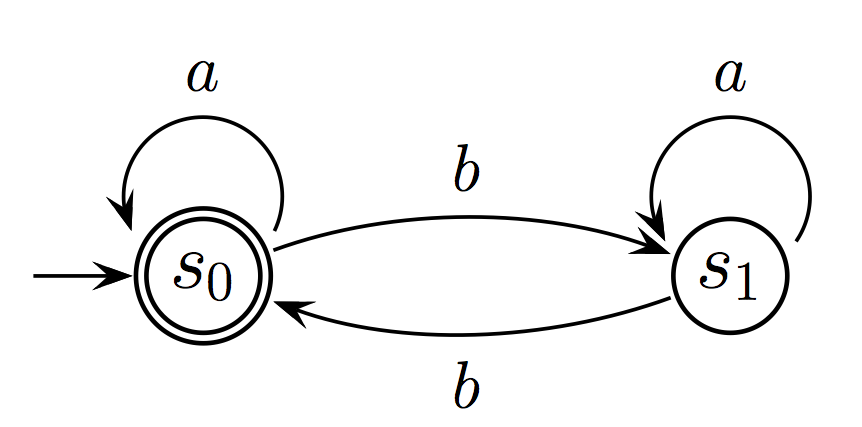   A3:

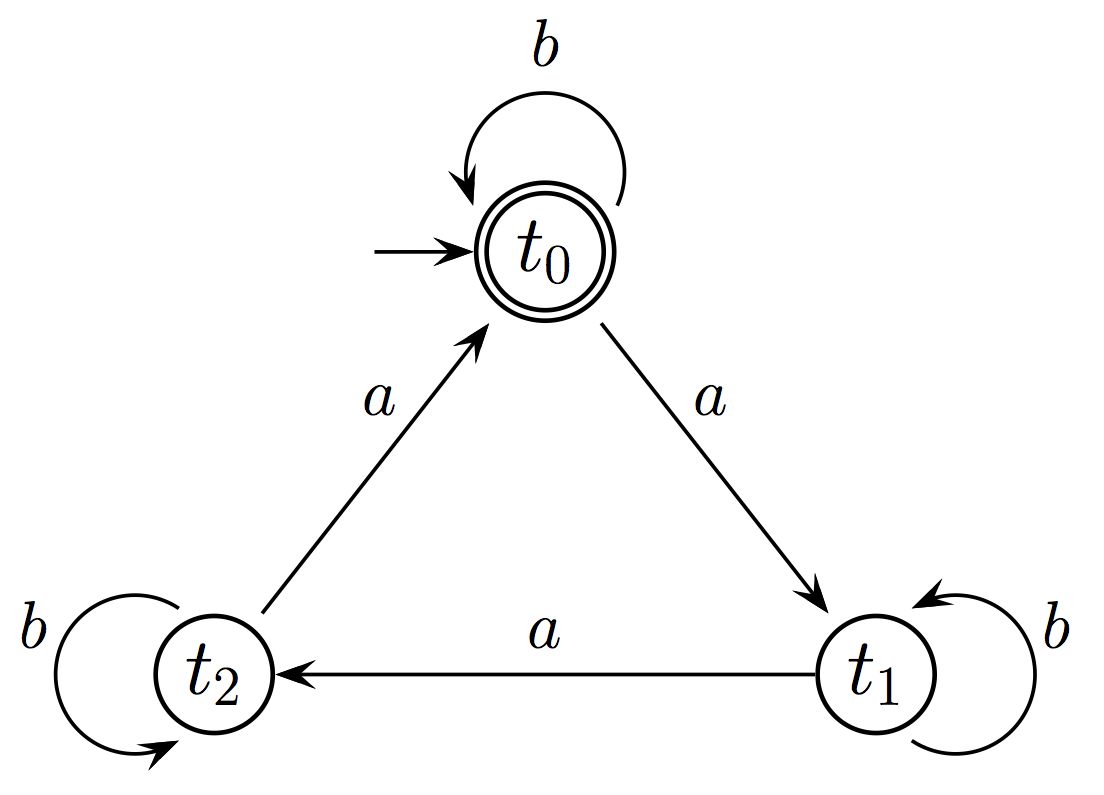   Construct a Büchi automaton, which accepts L(A₂) ∩ L(A₃).
5. Assume a finite automaton C. Prove the following statement:
   If L(C) does not contain the empty word then there is a Büchi automaton that recognizes the language L(C)^ω.
   Why is the precondition needed?

Homework 6, Thursday 19-4-2012

1. Let [a].φ, with φ a subformula, be the modal formula with meaning: for all possible a-steps you reach a state in which φ holds. Explain why this modality can be skipped in the treatment of the Hennessy-Milner Logic, by translating it into the other constructs of the language.
2. Give an example of a process that satisfies the formulas [a]⟨b⟩T and ⟨a⟩([b]⟨c⟩T) but does not satisfy [a]⟨b⟩⟨c⟩T.
3. In the paper available at http://www.cse.unsw.edu.au/~rvg/pub/spectrum1.ps.gz there are a number of pictures, called Counterexample 1, 2, 3, etc. For each of these counterexamples up to counterexample 8, provide a HML formula (if needed with infinite conjunctions) that holds for the left process, but not for the right one.
   A (bad) pdf of the paper is here.
4. Give an example of two processes that are language equivalent but not partial trace equivalent.
5. How do completed trace equivalence and simulation equivalence relate in the spectrum of equivalence relations. Is one finer than the other? Explain you answer.
6. Show, for labelled transition systems without termination predicate, that bisimulation equivalence is strictly finer than completed trace equivalence. This means that it makes strictly fewer identifications. This involves two things:
   • show that whenever two processes are bisimulation equivalent, they are surely also completed trace equivalent.
   • give an example of two processes that are completed trace equivalent but not bisimulation equivalent.
   Hint: use the example in the handout. Explain why it works.

Homework 7, Thursday 26-4-2012

1. Redo the bits of of Q3 of last week that you didn't get right. Also try counterexamples 10, 14 and 15.
2. Apply the partition refinement algorithm to counterexample 5 in that paper. How many rounds are needed to conclude whether the two processes are bisimulation equivalent?
3. Consider the processes c.(a.0 + b.0), c.τ.(a.0 + b.0), c.(τ.a.0 + b.0), c.(a.τ.0 + b.0), c.(τ.(a.0 + b.0) + a.0) and c.(τ.a.0 + b.0) + c.a.0.
   Which of these processes are branching bisimulation equivalent to each other, and why (or why not)?
4. Consider a more bureaucratic version of the relay race that was presented in class. This time runner 1 may only pass the stick to runner 2 in the presence of a bureaucrat, who is stationed halfway the start and finish. The bureaucrat will watch the transaction and subsequently make a note of it in his notebook, that will be kept for posterity. Consider a specification that mentions the start of the race (start), the delivery of the parcel (finish) and the making of the bureaucratic note (note). Describe the implementation in an appropriate system description language.
5. Consider a process called "gatekeeper" that makes sure that of 2 other processes "1" and "2", at most one is in its critical section. Its action are "hear request of process i to enter critical section", or "h(i)" for short; "admit process i into critical section", or "a(i)"; and "observe that process i exits the critical section", "e(i)". Here "i" can have the values 1 or 2. Keep in mind that each of the processes i may enter the critical section multiple times. The actions "h(i)", "a(i)" and "e(i)" all synchronise with corresponding actions from the processes 1 and 2. The gatekeeper should be able to hear a request in any state, subject to the restriction that each process will request entry in the critical section only once, until it has entered and exited the critical section.
   1. Draw a process graph describing the correct behaviour of the gatekeeper.
   2. Express the behaviour of the gatekeeper by a system of recursive equations.

Homework 8, Thursday 3-5-2012

1. How would you translate the CSP expressions (a ☐ b) ⊓ c and (a ⊓ b) ☐ c into CCS? Here I omitted trailing .0's.
2. Give an example of three processes, none of which are rooted BB equivalent, but all of which are BB equivalent.
3. Give a simple algorithm A that transforms process graphs G into A(G), such that A(G) and A(H) are rooted branching bisimulation equivalent if and only if G and H are branching bisimulation equivalent.
4. Sequencing is a binary operation defined on any process graphs; it starts with its second component as soon as its first component cannot do any further actions.
   Sequential composition, on the other hand, is defined on process graphs equipped with a state-labelling, where some states are marked with the symbol for successful termination, ✔. Here the second component starts only when the first one successfully terminates.
   1. Give a definition of sequencing as an operator on process graphs.
   2. Is sequencing compositional for partial trace equivalence? Give a counterexample, or show why.
   3. Is sequencing compositional for completed trace equivalence? Give a counterexample, or show why.
   4. Is sequential composition compositional for partial trace equivalence? Give a counterexample, or show why.
   5. Is sequential composition compositional for partial trace equivalence? Give a counterexample, or show why.
5. We did question 5a above in class, during the tutorial; using this, proceed with 5b.

Homework 9, Thursday 10-5-2012

1. Model the relay race in CSP.
2. Consider a process that performs the actions a, d and one out of c or b once each, subject to the following restrictions, and no others, so any sequence of actions that is not forbidden must be possible:
   • b and c can never occur in the same trace.
   • if c happens, it must be after a, and
   • a happens before d.
   1. Give a CSP expression for this process that uses at most one occurrence of a choice operator (☐ or ⊓).
   2. Give an ACP expression for this process that uses at most one +.
   3. Give a CCS expression for this process that uses at most one +. You may have to smuggle in an internal action τ to make this possible.
3. The priority operator θ_a<b always gives priority of the specific action b over the specific action a. It does so by deleting all a-transitions from a state when there is a b-transition from that state. So θ_a<b(a(a+b(a+c(ba+a)))) = ab(a+cba). Give a structural operational semantics of this operator.
4. Here is an operational semantics of the sequencing operator:

   x --a--> x' ------------------ (for x' != 0) x;y --a--> x';y

   x --a--> 0 ------------ x;y --a--> y

   Is it in GSOS format? What is wrong with this operational semantics? Show that strong bisimulation is not a congruence for this operator (in the context of CCS).
5. Give a structural operational semantics in GSOS format of the sequencing operator.
6. Modify the definition of completed trace semantics in five different ways, namely such that
   1. deadlock = livelock and fair divergence = progress,
   2. fair divergence = progress, and livelock differs from deadlock and from progress,
   3. deadlock = livelock and fair divergence differs from livelock and from progress,
   4. livelock = fair divergence, different from deadlock and progress,
   5. all four phenomena are distinguished.
   In all cases deadlock should be distinguished from normal progress.

Optional Extra Homework to make up for failed homework, Tuesday 15-5-2012

1. Consider the HML formula φ = [a]([b]⟨c⟩T) Give another HML formula without using the negation symbol, that holds for all processes for which φ does not hold.
2. Draw a spectrum of equivalence relations on processes with at least 5 different equivalences, indicating which equivalences are more discriminating than others. Give examples showing all differences between these equivalences.
3. Give a specification in ACP, CCS or CSP of a FIFO queue that can hold up to three bits of data. Each bit can be a 0 or a 1. The actions of the queue should be in(0), in(1), out(0) and in(1). The actions in(0), in(1) are always possible, unless the queue is full. The actions out(0) and in(1) are only possible if the oldest bit in the queue is a 0 or 1, respectively.
4. Let X be the process given by the recursive equation X = a.(b.X + c.X)
   and Y be the process given by the recursive equation Y = a.b.Y + a.c.Y.
   1. Draw the process graph representations of X and Y.
   2. Draw the process graph of the CSP process X ||_S Y where S is the set {a,b,c}.
   3. Draw the process graph of Y ||_S Y.
   4. Use the structural operational semantics of CSP to derive one of the transitions of X ||_S Y.
5. Use the partition refinement algorithm on the states of a.(a(a+aa)+aa)+aaa. With how many bisimulation equivalence classes do you end up?
6. Draw the graph of τ.(τ.(a+τ)+τ.a)+τ.(τ(a+τ)+a). Give a consistent colouring on the states of this graph that uses as few colours as possible.

Homework 10, Thursday 17-5-2012

1. Let Δ be the operator on processes that prepends a τ-loop at the beginning of its argument process. So a.Δb is a process with three states, one transition labelled a, one transition labelled b, and a τ-loop in the middle state.
   1. Give a structural operational semantics for this operator.
   2. Compare the processes a.Δ(b+τ.Δc) and a.Δ(b+τ.c) and a.(b+τ.Δc). Which of these processes are rooted branching bisimulation equivalent to each other? (Note that this can be seen as three questions.) Show bisimilarity by means of a consistent colouring.
   3. Which pairs of the above three processes are rooted branching bisimulation equivalent with explicit divergence? Show bisimilarity by means of a consistent colouring.
2. Give a Petri net for the following ACP expressions:
   1. a(b + c)
   2. a(b + c) || ad
   3. a(b + (c||d))
   4. a+X where X is given by the recursive equation X=aX.
   The communication function is given by γ(b,d)=a.
3. Show the strong bisimulation equivalence of the processes (a.b.c) || a and a.a.b.c + a.((a.b.c)+(b.(a||c))) using the equations of the axiomatisation of ACP only. These can be found in wikipedia.

More Optional Extra Homework to make up for failed homework

1. For which possible choices of Q and R are there transitions of the form a.(c+b.d) ||_{a,c} ((c+a) ||_{b} b) --a--> Q --b--> R in the labelled transition system of CSP? Give a proof tree of the formal derivation of one of those transitions from the structural operational rules of CSP.
   

Homework 11, Thursday 24-5-2012 (the last one)